Comment mesurer l’évolution des inégalités sociales à l’école : l’exemple de l’accès au bac
Il y a un demi-siècle, 45 % des enfants de cadres obtenaient le baccalauréat, contre seulement 5 % des enfants d’ouvriers. Désormais, 90 % des enfants de cadres l’obtiennent, contre 45 % des enfants d’ouvriers. Pierre Mercklé, sociologue, analyse les différents instruments de mesure de l’égalité des chances à l’école.
Publié le 4 octobre 2016
https://www.inegalites.fr/Comment-mesurer-l-evolution-des-inegalites-sociales-a-l-ecole-l-exemple-de-l - Reproduction interditeQue dire de l’évolution des inégalités sociales d’accès au baccalauréat ? La conclusion dépend largement de l’indicateur que l’on utilise.
Première mesure : les différences entre proportions
La façon la plus simple de mesurer une inégalité consiste à calculer la différence entre deux proportions. Il y a 50 ans, le taux d’obtention du baccalauréat était de 45 (enfants de cadres) – 5 (enfants d’ouvriers) = 40 points plus élevé chez les enfants de cadres que chez les enfants d’ouvriers. Si l’on veut mesurer les évolutions de la même façon, on peut très facilement vérifier que la proportion de bacheliers parmi les enfants de cadres a augmenté de 90–45= 45 points, tandis que parmi les enfants d’ouvriers, elle n’a augmenté que de 45–5= 40 points. Par conséquent, l’écart entre eux s’est accru.
| Taux de bacheliers selon la catégorie socioprofessionnelle des parents | ||
|---|---|---|
| Il y a 50 ans | Aujourd'hui | |
| Enfants de cadres | 45 % | 90 % |
| Enfants d'ouvriers | 5 % | 45 % |
Source : ministère de l'Education nationale - Enfants entrés en sixième en 1995.
– Mesurées par les différences entre proportions, les inégalités d’obtention du baccalauréat ont augmenté au cours des 50 dernières années.
Deuxième mesure : les rapports entre proportions
Il y a 50 ans, les enfants de cadres étaient neuf fois plus nombreux à obtenir le baccalauréat que les enfants d’ouvriers. Pour le vérifier, il suffit de faire le rapport entre 45 %, taux des enfants de cadres et 5 %, taux des enfants d’ouvriers (45 : 5 = 9).
En termes d’évolution, la proportion de bacheliers parmi les enfants de cadres a été multipliée par deux (90 % divisé par 45 %), tandis que parmi les ouvriers elle a été multipliée par neuf (45 % divisé par 5 %).
Par conséquent, le rapport entre leurs taux d’obtention du baccalauréat a diminué : il y a 50 ans, les enfants de cadres étaient neuf fois plus nombreux à être bacheliers que les enfants d’ouvriers, ils ne sont plus que deux fois plus nombreux (90 % divisé par 45 % =) aujourd’hui.
– Mesurées par les rapports entre proportions, les inégalités d’obtention du baccalauréat ont diminué au cours des 50 dernières années.
Troisième mesure : les taux de variation par rapport au maximum de variation possible
Le problème avec ces deux premières façons de mesurer les inégalités, c’est d’abord qu’elles se contredisent, et ensuite qu’elles ne sont pas adaptées à la comparaison de pourcentages, parce que ceux-ci. ne peuvent pas dépasser 100 %. Par exemple, pour maintenir un taux d’obtention du bac neuf fois plus élevé que celui des enfants d’ouvriers, les enfants de cadres devraient désormais être 405 % (45 x 9) à l’obtenir !
Il faut donc recourir à des mesures qui tiennent compte du fait que sur le chemin qui mène ne serait-ce qu’aux fameux « 80 % d’une classe d’âge au baccalauréat » (c’était l’objectif à l’horizon 2000, qui avait été fixé en 1985 par Jean-Pierre Chevènement, le ministre de l’Education de l’époque), les dernières longueurs sont plus difficiles à parcourir que les premières.
Pour en tenir compte, il y a une première mesure possible, qui consiste justement à comparer la variation réelle des pourcentages à la longueur du chemin qui restait à parcourir pour atteindre la proportion maximum de 100 %. Dans notre exemple, on voit ainsi qu’en 50 ans, les enfants de cadres ont amélioré leur taux d’obtention du bac de (90–45) 45 points, alors qu’ils pouvaient l’améliorer au maximum de (100–45=) 55 points. Ils l’ont donc amélioré de 82 % (45 divisé par 55 multiplié par 100 =) du maximum de variation possible.
De leur côté les enfants d’ouvriers ont amélioré leur taux d’obtention du baccalauréat de 40 points (45 – 5) divisé par 95 (100 – 5), soit 42 % seulement du maximum de variation possible. Les enfants de cadres ont réduit deux fois plus vite que les enfants d’ouvriers la distance qui les séparait de l’idéal des 100 % d’une classe d’âge au baccalauréat.
– Mesurées par les taux de variation par rapport au maximum de variation possible, les inégalités d’obtention du baccalauréat ont augmenté au cours des 50 dernières années.
Quatrième mesure : les « rapports de chances relatives »
Ce n’est pas ce taux de variation par rapport au maximum de variation possible qui s’est imposé parmi les sociologues pour mesurer les inégalités, mais plutôt une autre mesure qu’on appelle les « odds ratio » en anglais, ou en français les « rapports de chances relatives ». Pour comprendre de quoi il s’agit, il faut d’abord expliquer ce qu’est un « odds » ou « chance relative », et ensuite ce qu’est le rapport entre ces chances relatives.
Qu’est-ce qu’un « odds » ou « chance relative » ? Imaginez que 50 % des enfants de cadres obtiennent le bac (comme c’était en réalité le cas vers la fin des années 1960). Dans ce cas, 50 % d’entre eux ne l’obtiennent pas : on dira qu’il y a autant d’enfants de cadres qui obtiennent le bac que d’enfants de cadres qui ne l’obtiennent pas. Maintenant, si 75 % des enfants de cadres obtiennent le bac (comme c’était le cas cette fois dans les années 1980), alors 25 % des enfants de cadres ne l’obtiennent pas, et dans ce cas, on dira qu’il y a 3 fois (75 divisé par 25) plus d’enfants de cadres qui obtiennent le bac que d’enfants de cadres qui n’obtiennent pas le bac.
Reprenons maintenant les chiffres de notre exemple de départ et calculons les chances relatives d’avoir le bac (plutôt que de ne pas l’avoir) des enfants de cadres il y a 50 ans et aujourd’hui. Il y a 50 ans, les enfants de cadres étaient 45 % à avoir le bac et donc 55 % à ne pas l’avoir. Le rapport entre la probabilité d’avoir le bac (45 %) et celle de ne pas l’avoir (55 %) est égal à 45 divisé par 55 = 0,82 fois plus de chances d’obtenir le bac que de ne pas l’obtenir. Ou – ce qui revient au même – la proportion inverse : 1,22 fois moins de chance (55 divisé par 45) de ne pas avoir le bac que de l’avoir. Désormais ils ont neuf fois plus de chances de l’obtenir que de ne pas l’obtenir : 90 % (obtenir le bac) divisé par 10 % (ne pas l’obtenir).
Ces chiffres, ce sont des « odds » ou « chances relatives », qui s’obtiennent en divisant la probabilité d’être, de faire, ou de réussir quelque chose, par la probabilité contraire de ne pas l’être, ne pas le faire ou d’y échouer. Le terme « odds » vient de l’anglais et désigne à l’origine les « cotes » dans les paris sportifs dont les Britanniques sont friands : si vous voulez parier là-dessus, sachez que désormais les chances d’obtenir le bac pour les enfants de cadres sont de 9 contre 1 !
Ensuite, qu’est-ce qu’un « rapport » de chances relatives ? Pour les enfants de cadres, la chance relative d’obtenir le bac était donc de 0,82 contre 1 dans les années 1980, et de 9 contre 1 désormais. Et pour les enfants d’ouvriers ? Il y a 50 ans, 5 % des enfants d’ouvriers obtenaient le bac, et donc 95 % d’entre eux ne l’obtenaient pas. Donc leur chance relative d’avoir le bac était de 5 divisé par 95 = 0,052 contre 1. Ça veut dire que les enfants d’ouvriers avaient 0,052 fois plus de chances d’obtenir le bac que de ne pas l’obtenir. Ou dit beaucoup plus simplement, en calculant l’inverse, qu’ils avaient 19 fois (95 divisé par 5) plus de chances de ne pas obtenir le bac que de l’obtenir.
« L’odds ratio », c’est le « rapport » (ratio) entre les chances relatives des uns et de celles des autres, donc ici le rapport entre les chances relatives des enfants de cadres d’avoir le bac et celles des enfants d’ouvriers. Il y a 50 ans, cela donnait 0,82 (les chances relatives des cadres) divisé par 0,052 (les chances relatives des ouvriers) = 15,8 [1].
Comment exprimer cela clairement ? C’est assez simple : il y a 50 ans, les enfants de cadres avaient 15,8 fois plus de chances que les enfants d’ouvriers d’obtenir le baccalauréat plutôt que de ne pas l’obtenir.
Et aujourd’hui ? On fait le même calcul du rapport entre les chances relatives, ce qui donne 9 (les chances relatives des cadres) divisé par 0,82 (les chances relatives des ouvriers) = 11 [2]. Autrement dit, désormais, les enfants de cadres ont 11 fois plus de chances que les enfants d’ouvriers d’obtenir le baccalauréat plutôt que de ne pas l’obtenir.
– Mesurées par les « odds ratios », les inégalités d’obtention du baccalauréat entre enfants de cadres et enfants d’ouvriers ont diminué au cours des 50 dernières années, de 15 fois plus de chances relatives à 11 fois plus de chances relatives.
Quelle mesure faut-il utiliser ?
De tout ce qui précède, il ressort que nous disposons d’au moins quatre mesures qui donnent des conclusions contradictoires, soit « noires » (les inégalités ont augmenté), soit au contraire « roses » (elles ont diminué), pour reprendre les termes employés par le sociologue Jean-Claude Combessie dans le dernier des articles qu’il a consacrés à cette question [3]. Or, la thèse défendue par ce sociologue, décédé en 2010, ce n’est qu’aucune de ces mesures n’est « meilleure » ou plus valable que les autres. D’autres sociologues ne sont pas de cet avis [4], mais pour Jean-Claude Combessie, il n’y aurait en particulier aucune bonne raison « statistique » de préférer les « odds ratios » aux taux de variation par rapport au maximum de variation possible.
| Pourquoi les rapports de chances se sont imposés en sociologie ?
Pour Jean-Claude Combessie, si les rapports de chances relatives se sont imposés depuis les années 1990, en particulier parmi les sociologues de l’éducation qui en font une grande consommation, ce ne serait pas parce qu’ils mesureraient plus correctement les variations des inégalités, mais parce qu’ils les mesureraient de façon plus optimiste ! |
Quelle conclusion pratique faut-il en tirer ?
Pour y voir plus clair pratiquement, on peut garder l’exemple de l’évolution des inégalités d’obtention du baccalauréat, mais cette fois en examinant une série plus complète de données. Celle-ci n’est pas très facile à trouver, mais on peut se servir du graphique ci-dessous, publié dans la dernière édition de « L’état de l’école », une publication du ministère de l’Éducation nationale, pour tenter de la reconstituer :
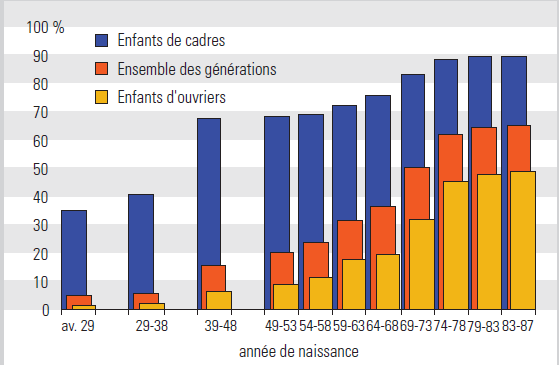
Source : ministère de l’Education nationale, l’état de l’école (édition 2010)
Dans le tableau ci-dessous, on a reconstitué les taux d’obtention du baccalauréat dans les générations successives d’enfants de cadres et d’enfants d’ouvriers dans les colonnes de gauche, et mesuré les inégalités entre ces taux avec les quatre mesures évoquées depuis le début de cet article dans les colonnes de droite :
| Les différentes mesures des inégalités d'accès au baccalauréat selon l'année de naissance | ||||||
|---|---|---|---|---|---|---|
| Taux d'accès au bac des enfants de cadres en % | Taux d'accès au bac des enfants d'ouvriers en % | Ecart | Rapport | Ecart cadres-ouvriers / écart taux d'accès ouvrier à 100 % de réussite en % | Odds ratio | |
| Avant 1929 | 35 | 1 | + 34 | x 35,0 | 34,3 | 53,3 |
| 1929-1938 | 41 | 2 | + 39 | x 20,5 | 39,8 | 34,1 |
| 1944-1948 | 67 | 6 | + 61 | x 11,2 | 64,9 | 31,8 |
| 1949-1953 | 68 | 9 | + 59 | x 7,6 | 64,8 | 21,5 |
| 1954-1958 | 69 | 11 | + 58 | x 6,3 | 65,2 | 18,0 |
| 1959-1963 | 72 | 17 | + 55 | x 4,2 | 66,3 | 12,6 |
| 1964-1968 | 75 | 20 | + 55 | x 2,6 | 68,8 | 12,0 |
| 1969-1973 | 83 | 32 | + 51 | x 2,6 | 75,0 | 10,4 |
| 1974-1978 | 88 | 45 | + 43 | x 2,0 | 78,2 | 9,0 |
| 1979-1983 | 90 | 47 | + 43 | x 1,9 | 81,1 | 10,1 |
| 1984-1988 | 89 | 49 | + 40 | x 1,8 | 78,4 | 8,4 |
Source : Calculs de Pierre Mercklé d'après les données du ministère de l'Education nationale
Qu’y voit-on ? Que dans l’ensemble, il n’arrive presque jamais aux rapports et aux « odds ratios » de rendre des « conclusions noires », alors que c’est très clairement le cas en particulier du rapport entre l’écart et l’écart maximum possible. Que faut-il faire dans ces cas-là ? Une position relativement simple consiste à favoriser l’éclectisme statistique, et donc à présenter les résultats de différentes mesures, en tout cas chaque fois qu’elles aboutissent à des conclusions divergentes. On indiquera ainsi par exemple qu’entre les enfants de cadres et les enfants d’ouvriers nés entre 1979 et 1983, et qui ont donc atteint l’âge normal du baccalauréat entre 1997 et 2001, les inégalités d’obtention du bac avaient diminué si l’on considère les « odds ratios », mais augmenté par rapport aux générations précédentes si l’on considère le rapport entre l’écart observé et l’écart maximum possible, sans qu’il soit possible de décider qu’un de ces deux indicateurs est « meilleur » que l’autre.
D’un côté, on peut dire par exemple que les « odds ratios » permettent de rendre compte de façon satisfaisante de la réduction de l’écart entre des valeurs dont les variations sont plafonnées, comme c’est le cas pour les pourcentages [5].
Mais de l’autre côté, le taux de variation par rapport au maximum de variation possible rend bien compte des perceptions subjectives des inégalités restantes que peuvent ressentir les individus : à mesure que leur situation s’améliore, par exemple en matière scolaire, les générations successives deviennent plus sensibles à des écarts plus petits, qui auraient auparavant été tenus pour négligeables.
Pierre Mercklé, sociologue, maître de conférences à l’ENS de Lyon et chercheur au Centre Max Weber (équipe « Dispositions, Pouvoirs, Cultures, Socialisations »). Article adapté du site de l’auteur, publié également sur www.idies.org.
[1] L’Odds ratio de 1960 = (45/(100-45))/(5/(100-5))=(45/55)/(5/95)=0,82/0,52=15,8.
[2] L’odss ratio de 2010 = (90/(100-90))/(45/(100-45))=(90/10)/(45/55)=9/0,82 = 11.
[3] « Analyse critique d’une histoire des traitements statistiques des inégalités de destin. Le cas de l’évolution des chances d’accès à l’enseignement supérieur », Jean-Claude Combessie, Actes de la recherche en sciences sociales n° 188, 2011, p. 4-31. Pour un article un peu moins récent, mais librement accessible en ligne, voir : « Trente ans de comparaison des inégalités des chances : quand la méthode retenue conditionne la conclusion », Jean-Claude Combessie, Courrier des statistiques 112, 2004, p. 37-54.
[4] Voir par exemple : « Sur l’origine, les bonnes raisons de l’usage, et la fécondité de l’odds ratio », Louis-André Vallet, Courrier des statistiques 121-122, 2007, p. 59-65.
[5] Et dans certains cas, comme le montre cet article L’inégal accès au bac des catégories sociales, ils peuvent même parfois rendre des conclusions noires en montrant par exemple que les chances relatives d’obtenir le bac ont augmenté plus vite pour les enfants d’enseignants que pour les enfants de pratiquement toutes les autres catégories sociales.
© Tous droits réservés - Observatoire des inégalités - (voir les modalités des droits de reproduction)


